Image d'une application

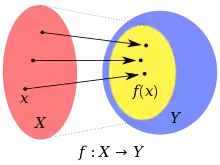
On appelle image d'une application f (d'un ensemble A vers un ensemble B) l'image directe par f de l'ensemble de départ A[1]. C'est donc le sous-ensemble de B contenant les images de tous les éléments de A, et uniquement ces images. On le note Im(f).

${\displaystyle \operatorname {Im} (f)=\{y\in B\mid \exists x\in A\quad f(x)=y\}=\{f(x)\mid x\in A\}=f(A)}$.

${\displaystyle f}$ est une fonction de ${\displaystyle X}$ dans ${\displaystyle Y}$. L'ovale jaune dans ${\displaystyle Y}$ est l'image de ${\displaystyle f}$.

Exemple : « L'image de la fonction sinus est le segment [–1, 1][1]. »[Note 1]

Une application est surjective si et seulement si son image coïncide avec son ensemble d'arrivée.

Une application est dite injective si tout élément de son ensemble d'arrivée a au plus un antécédent par f.

Une application est dite bijective si elle est à la fois surjective et injective, ce qui signifie que chaque élément de l'ensemble d'arrivée a un antécédent et que celui-ci est unique.

On peut aussi parler d'image réciproque d'une fonction qui est définie par:

${\displaystyle \operatorname {Im} (f^{-1})=\{x\in A\mid f(x)\in B\}=f^{-1}(B)}$