Image directe
L'image directe d'un sous-ensemble de par une application est le sous-ensemble de formé des éléments qui ont, par , au moins un antécédent appartenant à :
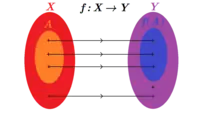
Schéma de l'image directe du sous-ensemble A d'une fonction injective mais non surjective (donc non bijective).
Exemples
- On définit en particulier l'image d'une application définie sur :
- On se gardera bien de confondre l'image directe par d'une partie de , avec l'image par d'un élément de , ou avec l'image de l'application [1].
- Considérons l'application de dans définie par , et . L'image directe de par est tandis que l'image de est .
Propriétés élémentaires
- Pour toutes parties et de ,
Plus généralement, pour toute famille de parties de , - Pour toutes parties et de ,
et cette inclusion peut être stricte, sauf si est injective[2].
On peut même prouver que est injective si et seulement si pour toutes parties et de , on a .
Plus généralement, pour toute famille non vide de parties de ,
- Toute partie de contient l'image directe de son image réciproque ; plus précisément[2] :
En particulier, si est surjective alors .
- On peut même prouver que est surjective si et seulement si pour toute partie de on a .
- (Une démonstration est proposée dans l'article Surjection.)
- Toute partie de est contenue dans l'image réciproque de son image directe :
et cette inclusion peut être stricte, sauf si est injective[2]. On peut même prouver que est injective si et seulement si pour toutes parties de , on a . - Si l'on considère de plus une application , alors l'image directe d'une partie de par la composée est :
Notes et références
- Pour éviter toute confusion, Saunders Mac Lane et Garrett Birkhoff, Algèbre [détail des éditions], vol. 1, p. 8, parlent d'une application ensembliste, qu'ils notent *.
- Pour une démonstration, voir par exemple le .
Articles connexes
- Théorie naïve des ensembles
- Image d'une partie par une fonction multivaluée (autrement dit : par une relation binaire)
- Portail des mathématiques
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons – Attribution – Partage à l’identique. Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.