Courbe de Lamé

Les courbes de Lamé (ou superellipses) sont un groupe de courbes définies pour la première fois par le mathématicien français Gabriel Lamé en 1818[1]. Elles sont définies par leur équation cartésienne :

\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1.

Exemples de courbes de Lamé

(n,a,b)=\left({\frac {1}{2}},1,1\right)

(n,a,b)=\left({\frac {3}{2}},1,1\right)

(n,a,b)=\left(4,1,1\right)

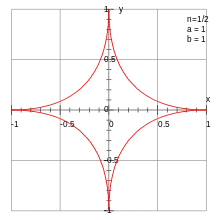
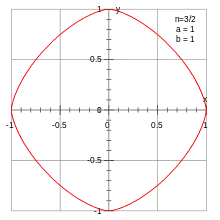
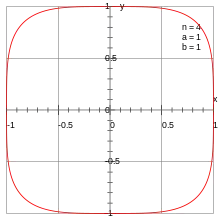
Similairement, elles sont définies par l'équation polaire (pour les points $(r,\theta )$ qui respectent l'équation) :

$r=\left(\left|{\frac {\cos(\theta )}{a}}\right|^{n}\!\!+\left|{\frac {\sin(\theta )}{b}}\right|^{n}\!\right)^{-1/n}\!,$

Propriétés

Les courbes de Lamé peuvent aussi être définies par l'équation paramétrique[2] :

{\begin{cases}x\left(\theta \right)&=\pm a\cos ^{\frac {2}{n}}\theta \\y\left(\theta \right)&=\pm b\sin ^{\frac {2}{n}}\theta \end{cases}}\qquad 0\leq \theta <{\frac {\pi }{2}}.

L'aire de la surface délimitée par une courbe de Lamé vaut[3]

${\frac {4^{\left(1-{\frac {1}{n}}\right)}ab{\sqrt {\pi }}\,\Gamma (1+{\frac {1}{n}})}{\Gamma ({\frac {1}{2}}+{\frac {1}{n}})}},$

où $Γ$ est la fonction Gamma.

Notes et références

(en) John J. O'Connor et Edmund F. Robertson, « Lamé Curves », sur MacTutor, université de St Andrews.
« Courbe de Lamé », sur mathcurve.
(en) Eric W. Weisstein, « Superellipse », sur MathWorld.

Articles connexes

Liens externes

Notices dans des dictionnaires ou encyclopédies généralistes :
- Den Store Danske Encyklopædi
- Store norske leksikon

Portail de la géométrie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons – Attribution – Partage à l’identique. Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.

[1] (en) John J. O'Connor et Edmund F. Robertson, « Lamé Curves », sur MacTutor, université de St Andrews.

[2] « Courbe de Lamé », sur mathcurve.

[3] (en) Eric W. Weisstein, « Superellipse », sur MathWorld.