Module d'élasticité isostatique

Généralement noté ${\displaystyle K}$ (${\displaystyle B}$ en anglais), le module d'élasticité isostatique permet d'exprimer la relation de proportionnalité entre le premier invariant du tenseur des contraintes et le premier invariant du tenseur des déformations :

${\displaystyle s=K\,e}$

où :

• ${\displaystyle s=\sum _{i}{\frac {1}{3}}\sigma _{ii}}$ est la contrainte isostatique (en unité de pression) ;
• ${\displaystyle K}$ est le module d'élasticité isostatique (en unité de pression) ;
• ${\displaystyle e=\sum _{i}\varepsilon _{ii}=\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}}$ est le taux de déformation isostatique[2] (sans dimension).

Il s'exprime, respectivement vis-à-vis des coefficients de Lamé ou du module de Young et du coefficient de Poisson, par :

${\displaystyle K=\lambda +{\frac {2}{3}}\,\mu ={\frac {1}{3}}\,{\frac {E}{(1-2\nu )}}}$.

Notes :

• pour ${\displaystyle \nu =1/3}$, ${\displaystyle K=E}$ ;
• pour ${\displaystyle \nu \to 1/2}$, ${\displaystyle K\to +\infty }$ (incompressibilité).

Les matériaux métalliques sont proches du premier cas (${\displaystyle K\approx E}$ dans leur domaine élastique) alors que les élastomères s'approchent d'un comportement incompressible (${\displaystyle K\gg E}$).

On peut aussi exprimer ${\displaystyle K}$ en fonction des modules d'élasticité en traction ${\displaystyle E}$ et en cisaillement ${\displaystyle G}$ :

${\displaystyle {\frac {1}{K}}={\frac {9}{E}}-{\frac {3}{G}}}$.

Le module d'élasticité isostatique représente la relation de proportionnalité entre la pression et le taux de variation du volume :

${\displaystyle \Delta P=-K\,{\frac {\Delta V}{V_{0}}}}$.

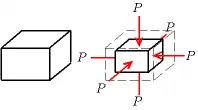
C'est l'inverse de la compressibilité isotherme ${\displaystyle \chi _{T}}$, définie en thermodynamique par :

${\displaystyle {\frac {1}{K}}=\chi _{T}=-{\frac {1}{V}}\,\left({\frac {\partial V}{\partial P}}\right)_{T}}$