Formules trigonométriques en kπ/7

Cet article présente des formules trigonométriques faisant intervenir des angles multiples de $π/7$ .

Valeur et construction approchées

Tracé (approximatif) d'un angle de

{\dfrac {\pi }{7}}

.

Le nombre $\cos {\frac {\pi }{7}}$ a pour développement décimal : $0{,}9009688...$ , suite A073052 de l'OEIS.

On a donc avec une assez bonne approximation :

\cos {\frac {\pi }{7}}\simeq {\frac {9}{10}}

.

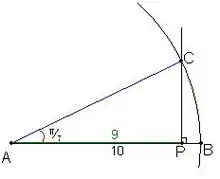
Cette valeur permet de construire à la règle et au compas un angle ayant une mesure proche de ${\frac {\pi }{7}}$ . On trace un segment [AB] et un point P tel que $AP={\frac {9}{10}}AB$ . Soit C le point d'interception entre le cercle de centre A et de rayon AB avec la perpendiculaire à (AB) passant par P. Alors l'angle ${\widehat {BAC}}$ a une mesure proche de ${\frac {\pi }{7}}$ .

Si on dispose sept cure-dents identiques de sorte que

A, X, Y, B

soient alignés, l'angle en $A$ vaut

\pi /7

.

Constructibilité

Le nombre $\cos {\frac {\pi }{7}}$ n'est pas constructible (on peut déduire ce cas particulier du théorème de Gauss-Wantzel, en utilisant le théorème de Wantzel et l'équation de degré 3 ci-dessous), ce qui revient à dire qu'il n'existe pas de construction à la règle et au compas de l'heptagone régulier.

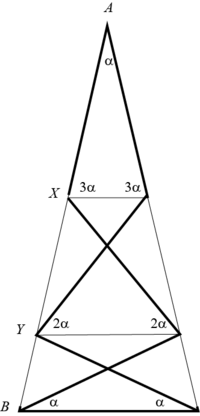
Par contre $\cos {\frac {\pi }{7}}$ est "cure-dents-constructible", comme indiqué dans la figure ci-contre [1]. Cette construction a été trouvée en 1973 par Crockett Johnson en jouant avec des cure-dents dans un café [2]. On peut aussi l'obtenir à partir d'un heptagone articulé avec des barres de même longueur.

Quelques solutions d'équations

L'équation $x^{3}-{\frac {x^{2}}{2}}-{\frac {x}{2}}+{\frac {1}{8}}=0$ a pour solutions :
$\cos {\frac {\pi }{7}},\quad -\cos {\frac {2\pi }{7}},\quad \cos {\frac {3\pi }{7}}$ [3] .

Démonstration

Remarquons que $\cos {\frac {4\pi }{7}}=\cos \left(\pi -{\frac {3\pi }{7}}\right)=-\cos {\frac {3\pi }{7}}$ ; $\theta ={\frac {\pi }{7}}$ est donc solution de

\cos 4\theta =-\cos 3\theta .\quad (1)

Cherchons les autres. (1) s'écrit $\cos 4\theta =\cos(\pi -3\theta )$ qui équivaut à $4\theta =\pi -3\theta +2k\pi$ ou $4\theta =3\theta -\pi +2k\pi$ , et on obtient $\theta ={\frac {\pi }{7}}+2k{\frac {\pi }{7}}$ ou $\theta =-\pi +2k\pi$ .

Si on pose $x=\cos \theta$ , on remarque donc que (1) équivaut à $x=\cos {\frac {\pi }{7}},\cos {\frac {3\pi }{7}},\cos {\frac {5\pi }{7}}=-\cos {\frac {2\pi }{7}},{\text{ou}}-1$ .

Or $\cos 4\theta =8x^{4}-8x^{2}+1$ et $\cos 3\theta =4x^{3}-3x$ .

Donc (1) équivaut à $8x^{4}+4x^{3}-8x^{2}-3x+1=0$ . $-1$ étant solution, on peut factoriser par $x+1$ et on obtient que

(1) équivaut à $(x+1)(8x^{3}-4x^{2}-4x+1)=0$ .

En divisant par 8, on obtient que $x^{3}-{\frac {x^{2}}{2}}-{\frac {x}{2}}+{\frac {1}{8}}=0$ a bien pour solutions $\cos {\frac {\pi }{7}},\cos {\frac {3\pi }{7}},-\cos {\frac {2\pi }{7}}$ .

$\cos {\frac {\pi }{7}}$ est donc un nombre algébrique, mais on peut montrer qu'il n'est pas exprimable par radicaux réels (l'équation ci-dessus présente un casus irreducibilis) ; on peut cependant l'exprimer par radicaux cubiques et carrés complexes : si $u={\frac {-1+3\mathrm {i} {\sqrt {3}}}{2}}$ , $\cos {\frac {\pi }{7}}={\frac {1}{6}}\left(1+{\sqrt[{3}]{\frac {49}{u}}}+{\sqrt[{3}]{7u}}\right)$ .

Donc l'équation $x^{3}-x^{2}-2x+1=0$ a pour solutions : $2\cos {\frac {\pi }{7}},-2\cos {\frac {2\pi }{7}},2\cos {\frac {3\pi }{7}}$ , ce qui montre que $2\cos {\frac {\pi }{7}}$ est un entier algébrique.
L'équation $x^{3}+x^{2}-x+{\frac {1}{7}}=0$ a pour solutions :
${\frac {\tan {\frac {\pi }{7}}}{\sqrt {7}}},\quad {\frac {\tan {\frac {2\pi }{7}}}{\sqrt {7}}},\quad -{\frac {\tan {\frac {3\pi }{7}}}{\sqrt {7}}}$ [3] .

Démonstration

En itérant la formule $\tan(a+b)={\frac {\tan a+\tan b}{1-\tan a\tan b}}$ , on obtient que $\tan 7\theta ={\frac {t(t^{6}-21t^{4}+35t^{2}-7)}{1-21t^{2}+25t^{4}-7t^{6}}}$ , où $t=\tan \theta$ .

Comme $\tan 7\theta =0\Leftrightarrow \theta =k\pi /7$ , les 6 solutions de $t^{6}-21t^{4}+35t^{2}-7=0$ sont $\pm \tan \pi /7,\pm \tan 2\pi /7,\pm \tan 3\pi /7$ .

En remplaçant $t$ par $x{\sqrt {7}}$ , on obtient que $49x^{6}-147x^{4}+35x^{2}-1=0$ a pour solutions $\pm {\frac {\tan \pi /7}{\sqrt {7}}},\pm {\frac {\tan 2\pi /7}{\sqrt {7}}},\pm {\frac {\tan 3\pi /7}{\sqrt {7}}}$ .

Or $49x^{6}-147x^{4}+35x^{2}-1=(7x^{3}-7x^{2}-7x-1)(7x^{3}+7x^{2}-7x+1)$ .

Une étude permet de déterminer que les solutions de $7x^{3}+7x^{2}-7x+1=0$ sont ${\frac {\tan {\frac {\pi }{7}}}{\sqrt {7}}},\quad {\frac {\tan {\frac {2\pi }{7}}}{\sqrt {7}}},\quad -{\frac {\tan {\frac {3\pi }{7}}}{\sqrt {7}}}$ et celles de $7x^{3}-7x^{2}-7x-1=0$ leurs opposées.

Donc l'équation $x^{3}+7x^{2}-49x+49=0$ a pour solutions : ${\sqrt {7}}\,\tan {\frac {\pi }{7}},{\sqrt {7}}\,{\tan {\frac {2\pi }{7}}},-{\sqrt {7}}\,\tan {\frac {3\pi }{7}}$ ce qui montre que ${\sqrt {7}}\tan {\frac {\pi }{7}}$ est un entier algébrique.
L'équation
$x^{3}+{\frac {x^{2}}{2}}-{\frac {1}{56}}=0$

a pour solutions :
${\frac {\sin {\frac {\pi }{7}}}{\sqrt {7}}},\quad -{\frac {\sin {\frac {2\pi }{7}}}{\sqrt {7}}},\quad -{\frac {\sin {\frac {3\pi }{7}}}{\sqrt {7}}}$ [4] .

Démonstration

Si $x={\frac {\tan \theta }{\sqrt {7}}}$ , alors $y={\frac {\sin(2\theta )}{\sqrt {7}}}={\frac {2x}{1+7x^{2}}}$ d'après la formule du sinus de l'angle double en fonction de la tangente.

Or pour $\theta =\pi /7,2\pi /7,-3\pi /7$ , l'équation précédente montre que $x^{2}(x+1)=x-1/7$ , donc $y={\frac {2x}{1+7x^{2}}}={\frac {2x}{1+7{\frac {x-1/7}{x+1}}}}={\frac {x+1}{4}}$ , et $x=4y-1$ .

Si donc on remplace $x$ par $4x-1$ , dans $x^{3}+x^{2}-x+{\frac {1}{7}}=0$ on obtient une équation vérifiée par ${\frac {\sin {\frac {2\pi }{7}}}{\sqrt {7}}},{\frac {\sin {\frac {4\pi }{7}}}{\sqrt {7}}}={\frac {\sin {\frac {3\pi }{7}}}{\sqrt {7}}},-{\frac {\sin {\frac {6\pi }{7}}}{\sqrt {7}}}=-{\frac {\sin {\frac {\pi }{7}}}{\sqrt {7}}}$ ; l'équation obtenue est $x^{3}-{\frac {x^{2}}{2}}+{\frac {1}{56}}=0$ .

En changeant $x$ en $-x$ , on obtient l'équation $x^{3}+{\frac {x^{2}}{2}}-{\frac {1}{56}}=0$ vérifiée par ${\frac {\sin {\frac {\pi }{7}}}{\sqrt {7}}},-{\frac {\sin {\frac {2\pi }{7}}}{\sqrt {7}}},-{\frac {\sin {\frac {3\pi }{7}}}{\sqrt {7}}}$ .

Formules homogènes

On en déduit les fonctions symétriques élémentaires associées aux équations précédentes :

${\begin{cases}\cos {\frac {\pi }{7}}-\cos {\frac {2\pi }{7}}+\cos {\frac {3\pi }{7}}={\frac {1}{2}}\\\cos {\frac {\pi }{7}}\cos {\frac {2\pi }{7}}\cos {\frac {3\pi }{7}}={\frac {1}{8}}\\\cos {\frac {\pi }{7}}\cos {\frac {2\pi }{7}}-\cos {\frac {\pi }{7}}\cos {\frac {3\pi }{7}}+\cos {\frac {2\pi }{7}}\cos {\frac {3\pi }{7}}={\frac {1}{2}}\end{cases}}$
${\begin{cases}\tan {\frac {\pi }{7}}+\tan {\frac {2\pi }{7}}-\tan {\frac {3\pi }{7}}=-{\sqrt {7}}\\\tan {\frac {\pi }{7}}\tan {\frac {2\pi }{7}}\tan {\frac {3\pi }{7}}={\sqrt {7}}\\\tan {\frac {\pi }{7}}\tan {\frac {2\pi }{7}}-\tan {\frac {\pi }{7}}\tan {\frac {3\pi }{7}}-\tan {\frac {2\pi }{7}}\tan {\frac {3\pi }{7}}=-7\end{cases}}$
${\begin{cases}\sin {\frac {\pi }{7}}-\sin {\frac {2\pi }{7}}-\sin {\frac {3\pi }{7}}=-{\frac {\sqrt {7}}{2}}\\\sin {\frac {\pi }{7}}\sin {\frac {2\pi }{7}}\sin {\frac {3\pi }{7}}={\frac {\sqrt {7}}{8}}\\\sin {\frac {\pi }{7}}\sin {\frac {2\pi }{7}}+\sin {\frac {\pi }{7}}\sin {\frac {3\pi }{7}}-\sin {\frac {2\pi }{7}}\sin {\frac {3\pi }{7}}=0\end{cases}}$

Autres relations

\cos {\frac {2\pi }{7}}=2\cos ^{2}{\frac {\pi }{7}}-1={\frac {1}{4\cos {\frac {\pi }{7}}-2}}

\cos {\frac {3\pi }{7}}=-\cos {\frac {4\pi }{7}}=1-2\cos ^{2}{\frac {2\pi }{7}}={\frac {1}{4\cos {\frac {2\pi }{7}}+2}}

\cos {\frac {\pi }{7}}=-\cos {\frac {6\pi }{7}}=1-2\cos ^{2}{\frac {3\pi }{7}}={\frac {1}{2-4\cos {\frac {3\pi }{7}}}}

Autres formules découlant des précédentes

Pour d'autres valeurs de l'entier $k$ dans $k π/7$ , on peut se ramener aux formules précédentes en tenant compte de la parité de $cos$ et de l'imparité de $sin$ et $tan$ , et du fait que

\cos(\pi -\theta )=-\cos \theta {\text{ et }}\sin(\pi -\theta )=\sin \theta

.

Sommes de Newton

La suite

p_{n}:=\left(2\cos {\frac {\pi }{7}}\right)^{n}+\left(-2\cos {\frac {2\pi }{7}}\right)^{n}+\left(2\cos {\frac {3\pi }{7}}\right)^{n}\quad (n\in \mathbb {Z} )

se déduit des polynômes symétriques élémentaires ci-dessus, dans ses valeurs initiales

p_{0}=3,\quad p_{1}=1,\quad p_{2}=5

et dans sa récurrence linéaire d'ordre 3 :

\forall n\in \mathbb {Z} \quad p_{n+3}-p_{n+2}-2p_{n+1}+p_{n}=0

.

Par exemple :

p_{3}=4,\quad p_{4}=13,\quad p_{5}=16,\quad p_{6}=38,\quad p_{7}=57

suite A096975 de l'OEIS, et

p_{-1}=2,\quad p_{-2}=6,\quad p_{-3}=11,\quad p_{-4}=26,\quad p_{-5}=57

suite A274975 de l'OEIS.

Tous les entiers $p n$ sont strictement positifs[5], les deux suites $(p_{n})_{n\geq 3}$ et $(p_{-n})_{n\geq 1}$ étant même strictement croissantes.

Voir aussi

Liens externes

(en) Eric W. Weisstein, « Trigonometry Angles--Pi/7 », sur MathWorld

Notes et références

David wells, Le dictionnaire Penguin des curiosités géométriques, Eyrolles, 1998, p. 93
(en) Philip Nel, « Crockett Johnson : Art »
Voir « Nombres algébriques de degré 3 » sur Wikiversité.
Voir cet exercice corrigé sur Wikiversité.
(en) Roman Witula, « Ramanujan type trigonometric formulas: the general form for the argument ${\frac {2\pi }{7}}$ », J. Integer Seq., vol. 12,‎ 2009 (lire en ligne).

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons – Attribution – Partage à l’identique. Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.

[1] David wells, Le dictionnaire Penguin des curiosités géométriques, Eyrolles, 1998, p. 93

[2] (en) Philip Nel, « Crockett Johnson : Art »

[tan+cos-3] Voir « Nombres algébriques de degré 3 » sur Wikiversité.

[4] Voir cet exercice corrigé sur Wikiversité.

[5] (en) Roman Witula, « Ramanujan type trigonometric formulas: the general form for the argument ${\frac {2\pi }{7}}$ », J. Integer Seq., vol. 12,‎ 2009 (lire en ligne).