Loi zêta
En théorie de probabilité et statistiques, la distribution zêta est une loi de probabilité discrète de paramètre [1]. Elle est aussi appelée loi de Pareto discrète[2], en lien avec la loi de Pareto.
| Zêta | |
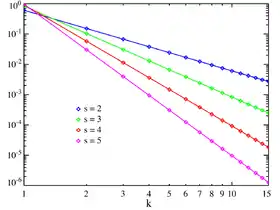 Fonction de masse | |
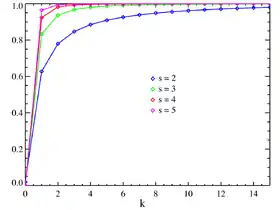 Fonction de répartition | |
Définition
On dit qu'une variable aléatoire suit une loi zêta de paramètre si :
où est la fonction zêta de Riemann non définie en 1[1].
Une loi zêta est un sous cas de la loi de Zipf où le paramètre N est infini.
Moments
Le n-ième moment est défini par l'espérance de Xn :
La série de droite est une représentation de la fonction zêta de Riemann et converge seulement pour les valeurs de s-n strictement supérieures à 1. Ainsi :
Lien avec la densité naturelle
Soit A une partie de , on dit que A a une densité naturelle si converge. Notons d(A) la limite. On a alors le résultat suivant :
Voir aussi
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Zeta distribution » (voir la liste des auteurs).
- Élise Davignon, « Introduction aux probabilités »
 [PDF], sur Université de Montréal
[PDF], sur Université de Montréal - « Programme probabilités discrètes »
 [PDF], sur université Paris Diderot
[PDF], sur université Paris Diderot
- Portail des probabilités et de la statistique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons – Attribution – Partage à l’identique. Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.