Coïncidence (informatique)

En informatique, l'opérateur logique coïncidence, également NON-OU exclusif (XNOR) et équivalence logique, peut se définir par la phrase suivante :

« La sortie est VRAI si et seulement si les deux entrées sont identiques ».

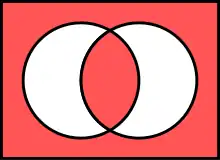Diagramme de Venn de

A\odot B

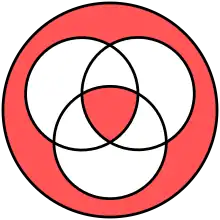Diagramme de Venn de la

coïncidence à trois entrées,
parfois notée $\bigodot (A,B,C)$ mais
qui n'est pas la même chose que
$A\odot B\odot C=(A\odot B)\odot C$
$=A\odot (B\odot C)$

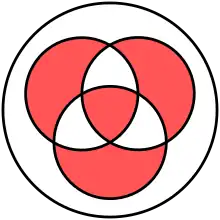Diagramme de Venn de

$A\odot B\odot C=(A\odot B)\odot C$
$~\odot ~$ $~\Leftrightarrow ~$
$=A\odot (B\odot C)$
$~\odot ~$ $~\Leftrightarrow ~$
identique à $A\oplus B\oplus C$
$=(A\oplus B)\oplus C$
$~\oplus ~$ $~\Leftrightarrow ~$
$=A\oplus (B\oplus C)$
$~\odot ~$ $~\Leftrightarrow ~$

On peut noter qu'il s'agit de la négation du OU exclusif, souvent noté XOR. On le nomme parfois (bien qu'abusivement) « identité » ou encore ET exclusif (XAND).

Son symbole est traditionnellement un point ("DOT" en anglais) dans un cercle : « ⊙ ».

Définition

Appelons A et B les deux opérandes considérés. Convenons de représenter leur valeur ainsi :

1 = VRAI

0 = FAUX

L'opérateur XNOR est défini par sa table de vérité, qui indique pour toutes les valeurs possibles de A et B la valeur du résultat S :

Entrée		Sortie
A	B	A XNOR B
0	0	1
0	1	0
1	0	0
1	1	1

Quelques propriétés mathématiques

$a\odot a=1$
$a\odot 0={\bar {a}}$
$a\odot 1=a$
$a\odot {\bar {a}}=0$
Commutativité $a\odot b=b\odot a$
Associativité $a\odot (b\odot c)=(a\odot b)\odot c=a\odot b\odot c$ mais $\bigodot (a,b,c)\neq a\odot b\odot c$
$a\odot b={\overline {a\oplus b}}$ et $a\odot b\odot c=a\oplus b\oplus c$ où $\oplus$ est le OU exclusif.
$a\odot b=ab+{\overline {a}}\cdot {\overline {b}}$
$a\odot b=0$ si et seulement si $a\neq b$

Application en électronique

Exemple d'utilisation : Le Circuit intégré 747266 TTL ou le circuit intégré CMOS 747266 intègre quatre portes logiques du type NON-OU exclusif. Illustration : Exemple : La lampe s'allume si l'on appuie sur rien, ou si l'on appuie sur « a » et « b » simultanément.

Équations: $S=a\odot b$; $S={\overline {a\oplus b}}$; $S=ab+{\overline {a}}{\overline {b}}$

Symbole IEC

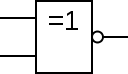
Symbole Informatique

En HTML, on le note ⊙.

En ASCII étendu, le code hexadécimal est 0x2299.

Voir aussi

Fonction logique
Fonction OUI
Fonction NON
Fonction ET
Fonction OU
Fonction NON-ET
Fonction NON-OU
Fonction OU exclusif
équivalence logique (doublon plus complet)

Portail de la logique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons – Attribution – Partage à l’identique. Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.