Approximation de Cornish-Fisher

L'approximation de Cornish-Fisher permet de transformer le quantile, ou une réalisation, d'une loi normale en une réalisation d'une loi dont l'asymétrie et le kurtosis en excès ne sont pas nuls. On la doit à Edmund Alfred Cornish et Ronald Aylmer Fisher[1].

Définition

On approche la réalisation Z de la loi voulue telle que :

F(Z)=\Phi (z_{c})

Où :

$F$ est la fonction de répartition de la loi $Z$
$\Phi$ est la fonction de répartition de la loi normale
$z_{c}$ est un quantile ou une réalisation de la loi normale

On a :

Z=z_{c}+(z_{c}^{2}-1){\frac {S}{6}}+(z_{c}^{3}-3z_{c}){\frac {K}{24}}-(2z_{c}^{3}-5z_{c}){\frac {S^{2}}{36}}

Où $S$ désigne l'asymétrie de la loi considérée, et $K$ , sa kurtosis en excès.

Domaine de validité

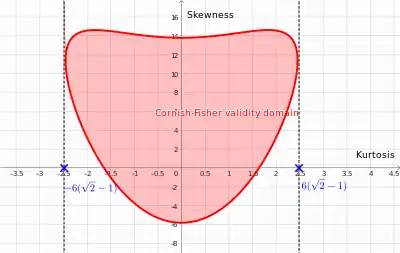
Domaine de validité de l'approximation de Cornish-Fisher

Pour que cette transformation marche elle doit être bijective. Une condition nécessaire et suffisante pour cela est que la dérivée ${\textstyle {\frac {{\rm {d}}Z}{{\rm {d}}z_{c}}}}$ ne s'annule pas, ce qui se traduit par

{\frac {S^{2}}{9}}-4\left({\frac {K}{8}}-{\frac {S^{2}}{6}}\right)\left(1-{\frac {K}{8}}+{\frac {5S^{2}}{36}}\right)\leq 0

Estimation du domaine de validité de l'approximation de Cornish-Fisher

On a :

{\frac {{\rm {d}}Z}{{\rm {d}}z_{c}}}=1+2z_{c}{\frac {S}{6}}+(3z_{c}^{2}-3){\frac {K}{24}}-(6z_{c}^{2}-5){\frac {S^{2}}{36}}=1-{\frac {K}{8}}+{\frac {5S^{2}}{36}}+{\frac {S}{3}}z_{c}+\left({\frac {K}{8}}-{\frac {S^{2}}{6}}\right)z_{c}^{2}.

Afin de garantir la positivité de ce terme, il faut que le discriminant de cette équation du second degré soit négatif :

\Delta (K)={\frac {S^{2}}{9}}-4\left(1-{\frac {K}{8}}+{\frac {5S^{2}}{36}}\right)\left({\frac {K}{8}}-{\frac {S^{2}}{6}}\right)={\frac {42S^{2}+5S^{4}}{54}}-{\frac {11S^{2}+36}{72}}K+{\frac {1}{16}}K^{2}\leqslant 0.

Pour que l'inégalité soit vérifiée, il faut que K soit entre les deux racines de cette deuxième équation du second degré, donc qu'elles existent, ce qui est vrai dans le cas :

\Delta ={\frac {(11S^{2}+36)^{2}}{5184}}-{\frac {42S^{2}+5S^{4}}{216}}={\frac {1}{5184}}S^{4}-{\frac {1}{24}}S^{2}+{\frac {1}{4}}={\frac {S^{4}-216S^{2}+1296}{5184}}\geqslant 0.

On a donc $S^{2}\leqslant 36(3-2{\sqrt {2}})$ ou $S^{2}\geqslant 36(3+2{\sqrt {2}})$ , soit $|S|\leqslant 6{\sqrt {3-2{\sqrt {2}}}}=6(-1+{\sqrt {2}})\approx 2,48$ ou $|S|\geqslant 6{\sqrt {3+2{\sqrt {2}}}}=6(1+{\sqrt {2}})\approx 14,48$ .

Le deuxième cas est impossible, donc on se restreint à l'intervalle $|S|\leqslant 6(-1+{\sqrt {2}})$ . On a alors :

{\begin{aligned}\Delta (K)\leqslant 0&\Longleftrightarrow &8(42S^{2}+5S^{4})-6(11S^{2}+36)K+27K^{2}\leqslant 0\\&\Longleftrightarrow &{\frac {(11S^{2}+36)-{\sqrt {S^{4}-1296S^{2}+7776}}}{9}}\leqslant K\leqslant {\frac {(11S^{2}+36)+{\sqrt {S^{4}-1296S^{2}+7776}}}{9}}.\end{aligned}}

En pratique en finance, $K$ et $S$ sont petits et $K$ est positif (variables leptokurtiques) ; la condition est donc respectée.

Notes et références

(en) E. A. Cornish et R. A. Fisher, « Moments and Cumulants in the Specification of Distributions », Revue de l'Institut international de statistique, vol. 5, n^o 4,‎ janvier 1938, p. 307-320 (JSTOR 1400905)

Liens externes

(en) Didier Maillard, « A User’s Guide to the Cornish Fisher Expansion » [PDF]
http://www.yats.com/doc/faits-stylises-ppt.pdf
http://www.northinfo.com/documents/189.pdf

Portail des probabilités et de la statistique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons – Attribution – Partage à l’identique. Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.

[1] (en) E. A. Cornish et R. A. Fisher, « Moments and Cumulants in the Specification of Distributions », Revue de l'Institut international de statistique, vol. 5, n^o 4,‎ janvier 1938, p. 307-320 (JSTOR 1400905)