42-graphe de Faulkner-Younger
Le 42-graphe de Faulkner-Younger est, en théorie des graphes, un graphe possédant 42 sommets et 63 arêtes.
| 42-graphe de Faulkner-Younger | |
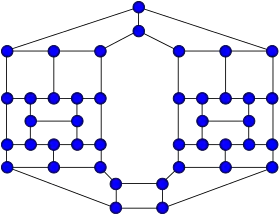 Représentation du 42-graphe de Faulkner-Younger. | |
| Nombre de sommets | 42 |
|---|---|
| Nombre d'arêtes | 63 |
| Distribution des degrés | 3 |
| Rayon | 6 |
| Diamètre | 9 |
| Maille | 4 |
| Automorphismes | 4 |
| Nombre chromatique | 3 |
| Indice chromatique | 3 |
| Propriétés | Planaire |
Propriétés
Propriétés générales
Le diamètre du 42-graphe de Faulkner-Younger, l'excentricité maximale de ses sommets, est 9, son rayon, l'excentricité minimale de ses sommets, est 6 et sa maille, la longueur de son plus court cycle, est 4. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.
Coloration
Le nombre chromatique du 42-graphe de Faulkner-Younger est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.
L'indice chromatique du 42-graphe de Faulkner-Younger est 3. Il existe donc une 3-coloration des arêtes du graphe telles que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Propriétés algébriques
Le groupe d'automorphismes du 42-graphe de Faulkner-Younger est un groupe abélien d'ordre 4.
Voir aussi
Liens internes
Liens externes
Références
- Portail des mathématiques